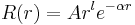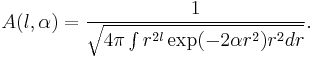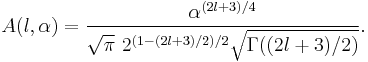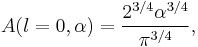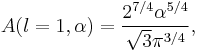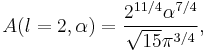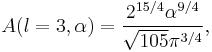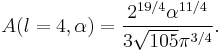Gaussian orbital

In computational chemistry and molecular physics, Gaussian orbitals (also known as Gaussian type orbitals, GTOs or Gaussians) are functions used as atomic orbitals in the LCAO method for the computation of electron orbitals in molecules and numerous properties that depend on these.[1]

Contents

Rationale

The principal reason for the use of Gaussian basis functions in molecular quantum chemical calculations is the 'Gaussian Product Theorem', which guarantees that the product of two GTOs centered on two different atoms is a finite sum of Gaussians centered on a point along the axis connecting them. In this manner, four-center integrals can be reduced to finite sums of two-center integrals, and in a next step to finite sums of one-center integrals. The speedup by 4--5 orders of magnitude compared to Slater orbitals more than outweighs the extra cost entailed by the larger number of basis functions generally required in a Gaussian calculation.

For reasons of convenience, many Gaussian integral evaluation programs work in a basis of Cartesian Gaussians even when spherical Gaussians are requested: the 'contaminants' are deleted a posteriori.

Slater radial orbitals read

\ R(r) = A r^l e^{-\alpha r}

Gaussian primitives for radial orbitals read

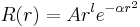\ R(r) = A r^l e^{-\alpha r^2},

where A is normalisation constant.

Using tables of Gaussian orbitals

There is a large database of Gaussian orbitals EMSL portal. The database determines shapes of (atom-centered) basis functions (in fact radial part of these function) optimised for one or the other criteria. The shapes are described as tables of factors and coefficients. The factors and coefficient define Gaussian primitives, which needs to be contracted (summed over) to determine a radial orbital. The basis functions possess a usual radial-angular decomposition

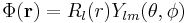\ \Phi(\mathbf{r}) = R_l(r) Y_{lm}(\theta,\phi),

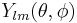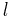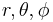where Y_{lm}(\theta,\phi) is spherical harmonic functions, l and m are angular momentum and projection of angular momentum quantum numbers, r,\theta,\phi are spherical coordinates. The function 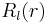R_l(r) is the radial orbital we want to determine. Radial orbital 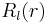R_l(r) is a sum of Gaussian primitives with an angular momentum factor in front of expression

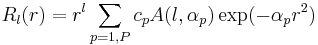\ R_l(r) = r^l \sum_{p=1,P} c_p A(l,\alpha_p) \exp(-\alpha_p r^2),

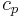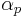where c_p and \alpha_p are listed in the tables of EMSL portal, the radial coordinate r must be in atomic units (see Bohr radius) and 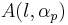A(l,\alpha_p) are normalisation factors to ensure the norm of Gaussian primitives 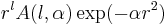r^l A(l,\alpha) \exp(-\alpha r^2) is one

A(l,\alpha) = \frac{1}{\sqrt{ 4\pi\int r^{2l} \exp(-2\alpha r^2) r^2 dr }}.

A closed form expression for normalisation factors 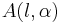A(l,\alpha) can be obtained using Gaussian integrals

A(l,\alpha) = \frac{\alpha^{(2l%2B3)/4}}{\sqrt{\pi}\ 2^{(1-(2l%2B3)/2)/2 } \sqrt{\Gamma((2l%2B3)/2)}}.

Particular values of the normalisation factor for different l are

A(l=0,\alpha) = \frac{2^{3/4}\alpha^{3/4}}{\pi^{3/4}},
A(l=1,\alpha) = \frac{2^{7/4}\alpha^{5/4}}{\sqrt{3}\pi^{3/4}},
A(l=2,\alpha) = \frac{2^{11/4}\alpha^{7/4}}{\sqrt{15}\pi^{3/4}},
A(l=3,\alpha) = \frac{2^{15/4}\alpha^{9/4}}{\sqrt{105}\pi^{3/4}},
A(l=4,\alpha) = \frac{2^{19/4}\alpha^{11/4}}{3\sqrt{105}\pi^{3/4}}.

Molecular integrals

Molecular integrals over Cartesian Gaussian functions were first proposed by Boys[2] in 1950. Since then much work has been done to speed up the evaluation of these integrals which are the slowest part of many quantum chemical calculations. McMurchie and Davidson (1978) introduced Hermite Gaussian functions to take advantage of differential relations.[3] Pople and Hehre (1978) developed a local coordinate method.[4] Obara and Saika introduced efficient recursion relations in 1985,[5] which was followed by the development of other important recurrence relations. Gill and Pople (1990) introduced a 'prism' algorithm which allowed efficient use of 20 different calculation paths.[6]

The POLYATOM System

The POLYATOM System[7] was the first package for ab initio calculations using Gaussian orbitals that was applied to a wide variety of molecules.[8] It was developed in Slater's Solid State and Molecular Theory Group (SSMTG) at MIT using the resources of the Cooperative Computing Laboratory. The mathematical infrastructure and operational software were developed by Imre Csizmadia,[9] Malcolm Harrison,[10] Jules Moskowitz[11] and Brian Sutcliffe.[12]

See also

References

  1. ^ Gill, Peter M.W. (1994). "Molecular integrals Over Gaussian Basis Functions". Advances in Quantum Chemistry 25: 141–205. Bibcode 1994AdQC...25..141G. doi:10.1016/S0065-3276(08)60019-2. http://cs.anu.edu.au/~Alistair.Rendell/hons09/qc/GillReview.pdf. Retrieved 17 June 2011. 
  2. ^ S.F. Boys, Proc. R. Soc. London Ser. A 200, 542 (1950)
  3. ^ McMurchie, Larry E.; Davidson, Ernest R. (1978). "One- and two-electron integrals over Cartesian Gaussian functions". Journal of Computational Physics 26 (2): 218–31. Bibcode 1978JCoPh..26..218M. doi:10.1016/0021-9991(78)90092-X. 
  4. ^ Pople, J. A.; Hehre, W. J. (1978). "Computation of electron repulsion integrals involving contracted Gaussian basis functions.". J. Comp. Phys. 27 (2): 161–168. Bibcode 1978JCoPh..27..161P. doi:10.1016/0021-9991(78)90001-3. 
  5. ^ Obara, S.; Saika, A. (1986). "Efficient recursive computation of molecular integrals over Cartesian Gaussian functions". J. Chem. Phys. 84 (7): 3963–74. Bibcode 1986JChPh..84.3963O. doi:10.1063/1.450106. 
  6. ^ Gill, Peter M. W.; Pople, John A. (December 1991). "The Prism Algorithm for Two-Electron Integrals". International Journal of Quantum Chemistry 40 (6): 753–772. doi:10.1002/qua.560400605. http://rscweb.anu.edu.au/~pgill/papers/026PRISM.pdf. Retrieved 17 June 2011. 
  7. ^ I.G. Csizmadia, M.C. Harrison, J.W. Moskowitz and B.T. Sutcliffe, Nonempirical LCAO-MO-SCF-CI calculations on organic molecules with gaussian-type functions. Introductory review and mathematical formalism, Theoretica Chimica Acta, 6, 191, 1966.
  8. ^ A.C. Wahl, Chemistry by computer, Scientific American, pages 54-70, April, 1970.
  9. ^ Imre Csizmadia, Professor Emeritus of Chemistry, University of Toronto, in Reviews in Computational Chemistry, vol.15, p.248
  10. ^ Malcolm C. Harrison, Professor of Computer Science, New York Univesity
  11. ^ Jules W. Moskowitz, Professor Emeritus of Chemistry, New York University
  12. ^ Brian T. Sutcliffe, Professor of Chemistry, York University

External links